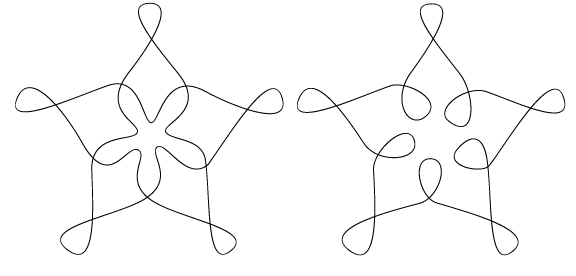
This pair of cross-sections is like the pair which bound section IV of the torus immersion. The critical point which lies between them would be a five-fold saddle (i.e. a starfish saddle?) The question is, can these two curves be unlooped into circles without pinching them? It turns out that they can't, because the one on the left has a winding number of 3. So, if this pair of cross-sections can't actually be unlooped, is there a similar pair which can? According to Prof. Banchoff's article, there might be, and if there are, then the surface that results has to be non-orientable.

All of that aside, what I really want to know is: what does the surface look like?