Welcome MeFites and Diggers! Since you folks are here looking for homework, I thought I’d dig up some other old ones I did for Prof. Banchoff’s calculus class. This one isn’t quite as involved as that other polynomial, but it was still fun to draw:

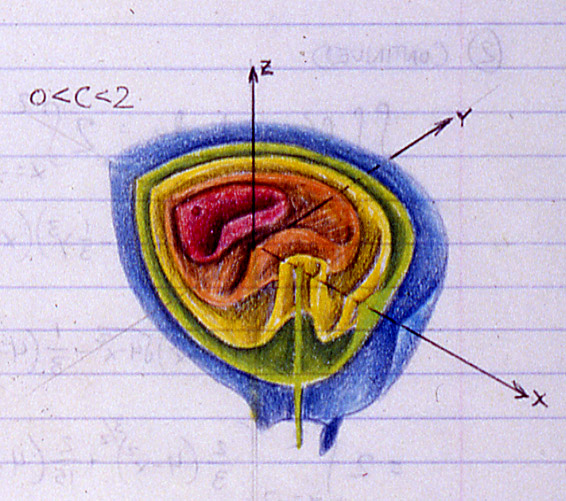
Detail. Click for the full page.

This is a visualization of some level surfaces of the equation G(x,y,z) = (4-x^2-y^2-z^2)*((x-c)^2+y^2). Another way to think of it is as the product of two distance fields, one from a sphere, and the other from a line, where the line’s distance from the center of the sphere is given by c. I don’t have an exact date for this, but it would have been sometime in the fall of 1988.