The other day at the office I was talking with some friends about animation, art, code, math. You know, the usual stuff. The subject of beauty came up, and it occurred to me that beauty, in all of these different disciplines, is often associated with elegant solutions to problems. Beautiful math explains complex phenomena with simple formulas, while beautiful animation accomplishes rich and layered storytelling goals with seemingly simple actions.
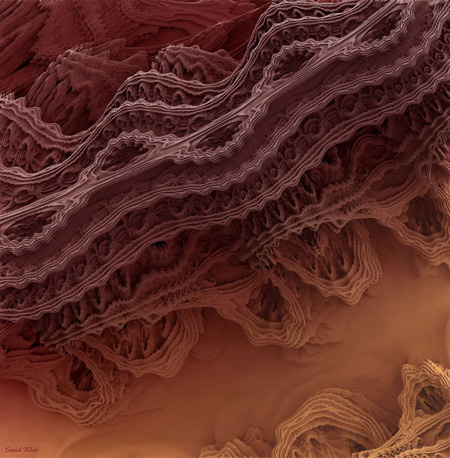
A couple of days later I stumbled on Daniel White’s amazing 3D fractal images, via my friend Saschka. I’ve been a fan of fractals since reading Mandelbrot’s book in high school. The Mandelbrot set is this rare creature that’s beautiful both mathematically (an elegant formula) and visually (rewarding exploration with endless variety). Like everybody else, I wondered whether something as beautiful could exist in three dimensions (or more, for that matter!) Until recently, though, nothing had turned up. There were beautiful shapes made using complex formulas, and elegant formulas that made ho-hum images, but nothing as sublime as Mandelbrot’s set. This thing, though, looks very promising!

If you like math even a little bit, it’s really worth reading White’s account of how these images got made. The guy wrote his own renderer, for crying out loud!
Daniel White doesn’t seem convinced yet that this object is the “real” 3D Mandelbrot, and I’m inclined to agree: as stunning as it is visually, there’s something a bit unwieldy about the formula, with all its thetas and phis. But what’s wonderful is the way White and his colleagues are conducting their search. They’re not content with just one kind of beauty. It won’t be “real” to them unless it has both!