Category Archives: math art
Interesting folding toys
Our friends in São Paulo gave our daughter these cute wooden folding toys. They’ve got elastic running through the middle, so you can twist the pieces around and make different shapes. After playing with them for a while, I noticed that they have an interesting mathematical property: when folded into any flat shape, any two triangles that meet are always the same color, forming a grid of diamonds (or squares, depending on your point of view.) I can’t help wondering why this is. It has something to do with the repeating pattern of four colors, obviously, but what?
4D Glasses T-shirt
Drew’s Fourth Dimension app has such a brilliant logo, I just had to have it on a T-shirt. Now you can have one too! We’re picky about our T-shirts, so we made this one exactly what we’d want to wear ourselves. It’s printed in a four-color process with a soft white ink underlayer, which gives a good balance of image quality and detail, while still looking and feeling good on a black shirt. There’s no text or other clutter, just the 4D glasses image, which speaks for itself. Enjoy!
Prime factorization sweater
Certified math nut Sondra Eklund has made an awesome sweater. Before you read her explanation, take a look at it and see if you can figure out how it works.
Of course, the synesthete in me says her color choices are all wrong. But she’s coloring a different animal here (primes, not numerals) so there’s no real way to be “right”. Regardless, I want this as a T-shirt!
(via MetaFilter)
The Fourth Dimension (for your phone)
If you look closely at my friend Drew Olbrich, you might notice something strange about him. He doesn’t like to talk about it, but: the part of Drew you can see is just an infinitesimal slice of a much higher-dimensional being.
To give the rest of us a sense of what it’s like to be him, Drew’s written a nifty little app (for your iPhone or iPad) called The Fourth Dimension. Give it a spin, and see if it doesn’t thicken your mind up just a little bit.
On beautiful math that makes beautiful art
The other day at the office I was talking with some friends about animation, art, code, math. You know, the usual stuff. The subject of beauty came up, and it occurred to me that beauty, in all of these different disciplines, is often associated with elegant solutions to problems. Beautiful math explains complex phenomena with simple formulas, while beautiful animation accomplishes rich and layered storytelling goals with seemingly simple actions.
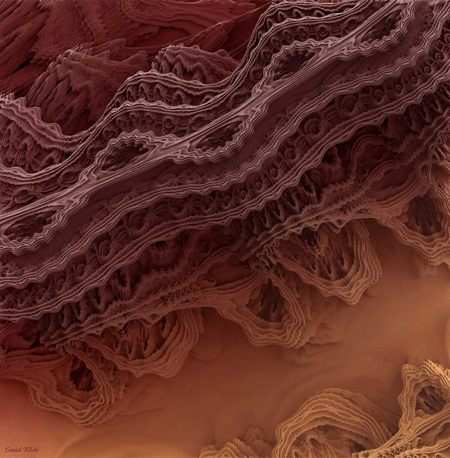
A couple of days later I stumbled on Daniel White’s amazing 3D fractal images, via my friend Saschka. I’ve been a fan of fractals since reading Mandelbrot’s book
If you like math even a little bit, it’s really worth reading White’s account of how these images got made. The guy wrote his own renderer, for crying out loud!
Daniel White doesn’t seem convinced yet that this object is the “real” 3D Mandelbrot, and I’m inclined to agree: as stunning as it is visually, there’s something a bit unwieldy about the formula, with all its thetas and phis. But what’s wonderful is the way White and his colleagues are conducting their search. They’re not content with just one kind of beauty. It won’t be “real” to them unless it has both!
Christian Faur’s crayon synesthesia
Christian Faur is an artist who makes these wonderful image-sculptures out of custom-cast crayons. The work itself is very Rungy Chungy and appealing to the eye. And Faur apparently has a thing for certain mathematicians. But it also turns out that he’s encoded synesthetic messages into several of his pieces:
Further, I have developed a mapping system that translates the English alphabet into twenty six discrete colors and I use these crayon “fonts” to add words and language to each of the pieces in the show… The direct representation of language in each piece further imbues the works with meaning and brings an aspect of color into each composition reminiscent of DNA coding. The alphabetic key at the lower left of each panel allows the viewer to interpret the individual words written throughout the various panels.
I gather that Faur does not actually have synesthesia himself, but this system makes perfect sense to me. If only he’d chosen his colors differently, I might be able to read the text straight up without the key! (Although it’s pleasing to note that his C, E, and Z are all perfect matches for my own.)
(via Drawn)
I want a triple-twist Klein bottle!
Here’s a great thing: a trio of Klein bottles nested one inside the other by mathematical glass-blower Alan Bennett (found via BoingBoing, of course.) You can tell it’s three separate bottles by looking at how the layers are interconnected: the long skinny tubes at the bottom each connect a pair of layers, and the folded-over edges at the top connect the same pairs (1+6, 2+5, 3+4). Figuring that out was fun, but then I saw this tantalizing quote from the museum’s website:
“In the series Alan Bennett made Klein bottles analogous to Mobius strips with odd numbers of twists greater than one.”
Darn, I was really hoping to see one of those! Suddenly the math geek in me is sorely disappointed. Given how much labor it must have taken to build this object, he could have made it a lot more interesting just by switching which tubes connect to which bottles! If the tubes linked 2+6, 3+5, and 1+4, this object would be transformed from three separate surfaces into a single surface that turns inside-out three times, the equivalent of a triply-twisted Moebius strip.
More math art
Welcome MeFites and Diggers! Since you folks are here looking for homework, I thought I’d dig up some other old ones I did for Prof. Banchoff’s calculus class. This one isn’t quite as involved as that other polynomial, but it was still fun to draw:
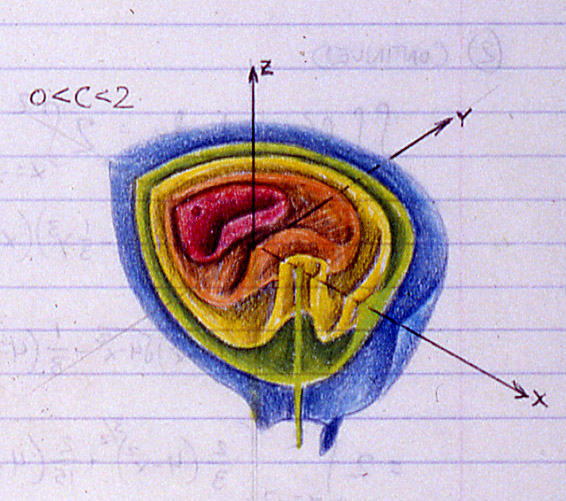
Detail. Click for the full page.
This is a visualization of some level surfaces of the equation G(x,y,z) = (4-x^2-y^2-z^2)*((x-c)^2+y^2). Another way to think of it is as the product of two distance fields, one from a sphere, and the other from a line, where the line’s distance from the center of the sphere is given by c. I don’t have an exact date for this, but it would have been sometime in the fall of 1988.
Knitting a Möbius Strip
The great confluence of geeky and crafty continues! Jacob Haller is knitting a Moebius Strip. With purple yarn, no less. I stumbled upon it while searching for images for this conversation about edgeless jigsaw puzzles.
Makes me glad to be alive, this does.